Теория семплирования сигналов
Семплирование в развитии электронной музыки сыграло очевидно огромную роль, да так, что отдельные семплеры даже породили абсолютно новые поджанры. Предлагаем поговорить о теории, стоящей за искусством семплирования, и, наконец, разобраться что же значат килогерцы и килобиты в характеристиках аудиофайлов.
Теорема отсчетов Найквиста-Шеннона
Аудиосемплинг основан на технологии диджитал-аудио, основные принципы которой были установлены еще в 1928 году инженером-электронщиком Гарри Найквистом и усовершенствованы в конце 1940-х годов математиком, инженером и криптографом Клодом Шенноном. Их идеи теперь известны как теорема отсчетов Найквиста-Шеннона (в русскоязычной литературе — теорема Котельникова), которая описывает преобразование непрерывного сигнала в серию дискретных значений, из которых можно воссоздать исходный сигнал.Очевидно, что это именно то, что нужно для преобразования аналогового звука (непрерывного сигнала) в цифровые данные (ряд дискретных значений) и наоборот.
Основной принцип дискретизации сигнала очень прост: это всего лишь измерение амплитуды сигнала через регулярные промежутки времени. Но процесс выборки и оцифровки аналогового сигнала требует двух важных аппроксимаций. Во-первых, измеренное значение не является мгновенным, а представляет собой среднее значение амплитуды сигнала в течение периода времени измерения. Это ведет к тому, что какие-либо мелкие скачки сигнала в течение этого периода будут потеряны.
Во-вторых, двоичные значения обладают такой характеристикой, как «разрешение» или точность, которая определяется количеством битов данных, которые объединяются для представления большего значения — байта. Каждый «бит» может иметь значение ноль или единицу, а байт объединяет определенное количество битов. Например, 8-битный байт может представлять целочисленные значения в диапазоне от 0 до 255 — всего 256 возможных значений — и поэтому любой аналоговый сигнал, преобразованный в 8-битное значение, должен быть округлен и аппроксимирован («квантизирован») на эту шкалу.
Теорема Найквиста-Шеннона позволяет нам выяснить, как часто и как точно нужно измерять значения сигнала источника, чтобы позже исходная форма волны была восстановлена с приемлемой точностью. Мы знаем эти факторы как частоту дискретизации (sample rate) и битовую глубину/разрядность (bit depth) соответственно.
Наложение спектров
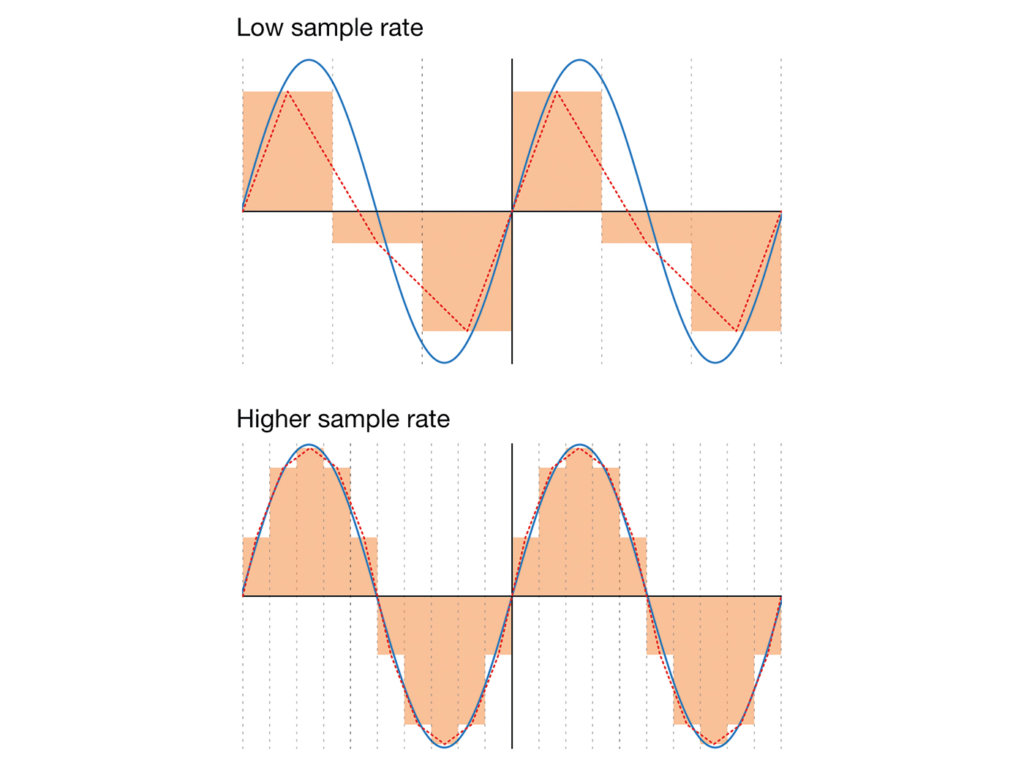
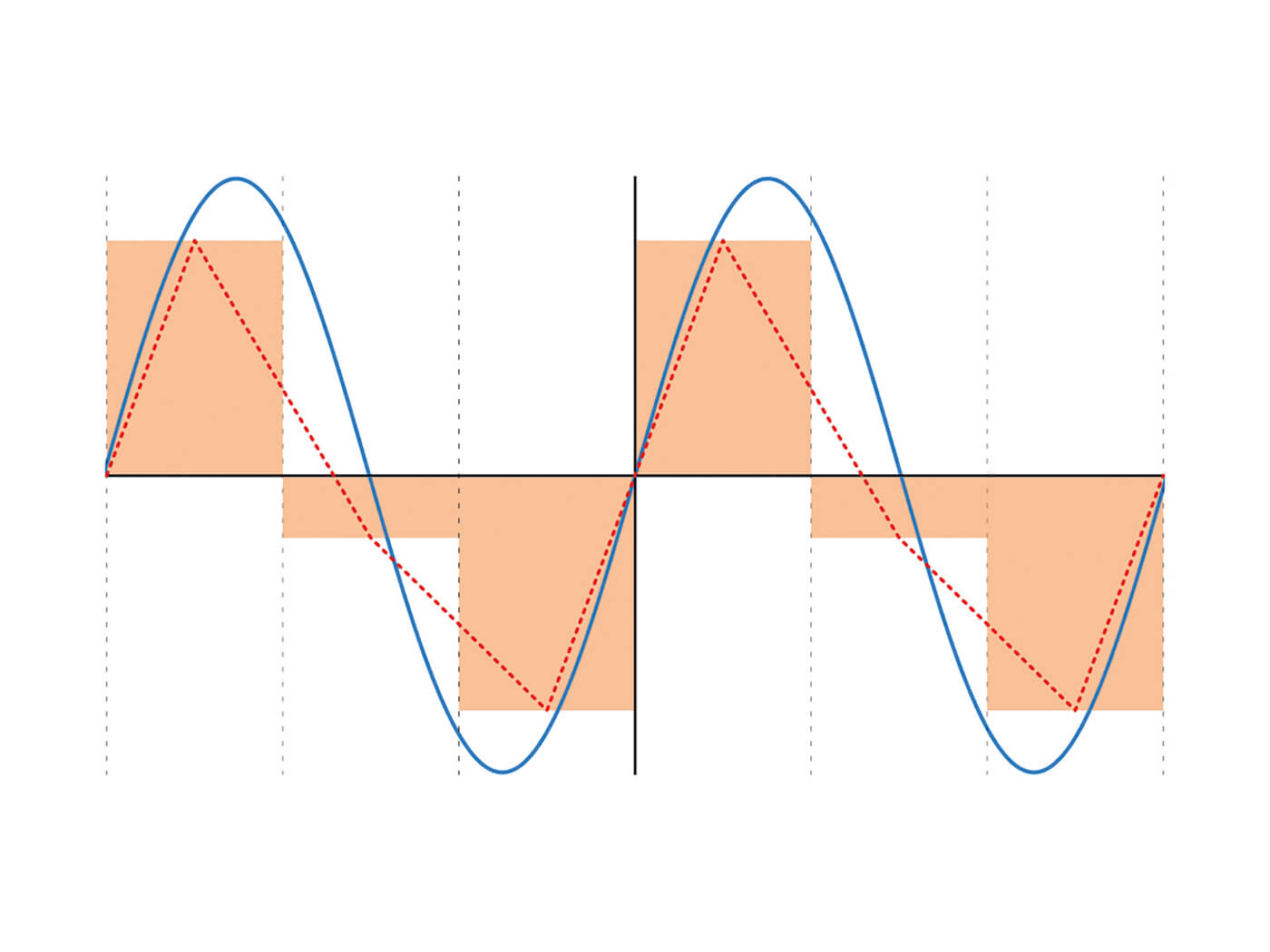
Наложение спектров возникает, когда частота дискретизации ниже предела Найквиста. На диаграмме выше сетка представляет собой частоту дискретизации, синяя линия — форму сигнала источника, а оранжевые блоки — семплированные значения. Красная линия является иллюстрацией того, насколько сильно восстановленная форма волны может отличаться от источника. В реальной системе восстановленная форма волны будет намного более гладкой, чем эта.
Несмотря на то, что современные системы цифрового аудио позволяют нам в значительной степени игнорировать такие детали, некоторые любители раритета все еще продолжают работать с классическими Akai MPC, E-MU Emulator или чем-то подобным, где такие допущения имеют критическое значение для эффективного управления памятью устройства. Давайте разберемся, почему современные стандарты частоты дискретизации и разрядности такие, какие они есть, и как они влияют на конечный аудиосигнал.
Частота дискретизации определяет максимальную частоту, с которой цифровая аудиосистема может точно считывать данные. Это связано с тем, что любые изменения амплитуды и, следовательно, частот звука внутри формы сигнала источника, которые происходят в течение более короткого периода, чем период выборки, будут потеряны при измерении амплитуды. Это приводит к искажению формы волны, известной как «Наложение спектров», которое проявляется как странный, высокий скрип при восстановлении формы волны.
Чтобы избежать наложения спектров нужно обеспечить достаточно высокую частоту дискретизации для захвата всех изменений частот исходного звука (или, по крайней мере, всех тех, которые нам важны). Мы можем сделать это, рассчитав «предел Найквиста» для сигнала и использовать это значение в качестве частоты дискретизации. По сути, предел Найквиста должен в два раза превышать максимальную частоту, которую нужно записать, поэтому, если семплировать басовый звук, не содержащий частот выше 10 кГц, предел Найквиста, а, следовательно, и оптимальная частота дискретизации звука будет составлять 20 кГц.
Однако даже преимущественно басовые звуки могут содержать в себе гармоники, которые простираются далеко в верхний регистр. Часто такие гармоники практически ничего не дают конечному звуку, но могут привести к наложению спектров, если семплируются с слишком низкой частотой.
Решение этой проблемы заключается в том, чтобы пропустить исходный звук через низкочастотный фильтр перед семплированием. Это уберет все несильно важные высокие частоты и, таким образом, позволит безопасно от наложения спектров использовать более низкие частоты дискретизации. Такая цепочка также позволяет легко оценить частоту дискретизации, с которой нужно записывать звук. Например, если вы пропускаете источник через низкочастотный фильтр со срезом 5 кГц, то вы знаете, что предел Найквиста будет около 10 кГц.
Предел Найквиста также определил так называемое «CD-качество», которое имеет частоту дискретизации 44,1 кГц: она в два раза превышает верхний предел человеческого слуха, равный примерно 20 кГц. Еще более высокая частота дискретизации, используемая в студии, обеспечивает еще большую точность воспроизводимых частот.
То, что предел нашего слуха ограничен 20 кГц, не значит, что нет смысла использовать большие частоты дискретизации. Дело в том, что они фиксируют все тонкости формы волны источника с высокой степенью точности и исключают любое оставшееся наложение на очень высоких частотах. Это исключит любое негативное влияния на слышимой полосе частот. В любом случае, все наложения могут быть легко отфильтрованы с помощью цифро-аналоговых преобразователей.
Ошибка квантизации
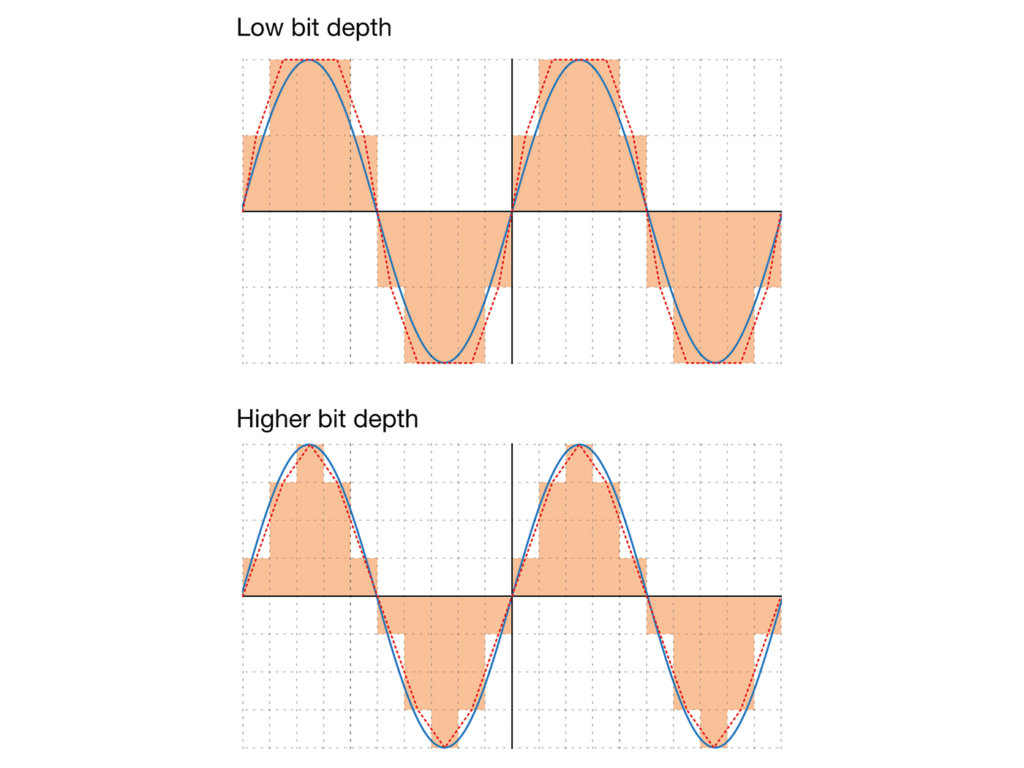
Ошибка квантизации является побочным эффектом разрядности. На рисунке выше сетка показывает частоту дискретизации (x) и квантизация (y). Опять же, синяя линия представляет собой форму сигнала источника, а оранжевые блоки — семплированые значения. Красная линия иллюстрирует восстановленную форму и то, как она отличается от исходной. Более низкая битовая глубина приводит к более высокому уровню шума. Слишком низкие битовые глубины приводят к зернистому искаженному звучанию.
Как уже упоминалось, разрядность цифрового семпла определяет диапазон значений, которые он может представлять. Принимая во внимание, что форма сигнала колеблется между отрицательными и положительными значениями, и что при полной амплитуде 8-битный сигнал имеет значение 0 или 255, тишина наступает на отметке 127 (т.е. средняя точка между 0 и 255), а все промежуточные значения квантизируются по этой шкале 0-255.
Другими словами, разрядность определяет разницу между самыми тихими и самыми громкими сигналами в системе или, так называемый, динамический диапазон системы. В 8-битной системе это примерно 48 дБ. Повышение до 16-бит значительно увеличивает диапазон значений от 0 до 65,535 и результирующий динамический диапазон около 96 дБ. Переход на 24-разрядный режим дает 16 777 216 возможных значений и динамический диапазон 144 дБ.
С увеличением разрядности точность квантизации улучшается, но всегда останется небольшая погрешность. Такая погрешность называется ошибкой квантизации. На слух она проявляется, как некоторая грязь или зернистость в восстановленной форме волны. Но опять же, как и в случае с пределом Найквиста, битовая глубина может быть оптимизирована. Короткие звуки с небольшой динамической детализацией могут быть семплированы на более низких битовых глубинах, но с увеличением динамики, соответственно, должна возрастать битовая глубина.
Цифро-аналоговые преобразователи оснащены различными приемами, чтобы сгладить и уменьшить искажения, вызванные ошибкой квантизации. Но, в целом, они всегда более заметны на низких разрешениях, чем на более высоких.
Ошибка квантизации на самом деле может оказывать весьма приятный эффект. Она подарила старым 8- и 12-битным семплерами, таким как Ensoniq Mirage и Akai S900, определенный звуковой характер, которого позднее очень не хватало в 16-битных семплерах. В наши дни тот же эффект можно воспроизвести с помощью биткраш-искажения.
Оригинальная статья
- Комментарии
Загрузка комментариев...


